Здравствуйте, друзья!
В сегодняшней небольшой статье немного пройдемся по теоретическим основам и коснемся одной из важнейших характеристик полета летательных аппаратов на большой скорости, в том числе и сверхзвуковой.
Сверхзвук и число Маха… Эти два понятия довольно тесно связаны и в наше время нет, наверное, ни одного человека, который бы так или иначе не слышал о числе М. Обычно этот термин сопровождает характеристики любого сверхзвукового (и даже просто скоростного) самолета. А самолетов таких у в мире сейчас немало и число их, я думаю, вряд ли будет уменьшаться :-).
Но ведь еще совсем не так давно теория сверхзвуковых течений была именно теорией, к тому же делающей, всего лишь, первые шаги. Фундаментальные основы она начала приобретать только около 140 лет назад, когда немецкий ученый и философ Эрнст Мах занялся исследованиями аэродинамических процессов при сверхзвуковом движении тел. В тот период он открыл и исследовал некоторые явления аэродинамики сверхзвука, получившие впоследствии свое название в его честь. В их ряду стоит и число Маха.
Интересен тот факт, что в советской науке (и в научной литературе, в особенности до войны и сразу после нее) этот термин часто употреблялся либо без расшифровки (просто число М, слово «Мах» не употеблялось), либо с использованием второй фамилии — Маиевский. То есть число Маха-Маиевского.
Все это было следствием нашего тогдашнего идеологического состояния. Эрнст Мах по своим философским взглядам (он был, по словам В.И.Ленина «субъективным идеалистом») не очень-то вписывался в рамки марксистско-ленинской философии, а Н.В.Маиевский был русским ученым, который занимался, в частности, проблемами внешней баллистики.
Внешняя баллистика — наука, исследующая движение тел после их выхода из устройства, придавшего им это движение, то есть, например, полет снаряда после его выхода из ствола артиллерийского орудия. Снаряд при этом летит с очень большой скоростью, в том числе и сверхзвуковой.
Вполне закономерно, что Н.В.Маиевский в своих исследованиях и разработках (передовых для своего времени и ставших впоследствии фундаментальными) оперировал понятием, аналогичным числу Маха, причем лет на 15 раньше своего немецкого коллеги.
А самое главное (для официальной идеологии :-)) было то, что русский ученый не был философом 🙂 и не имел взглядов, противоречащих марксистско-ленинской науке 🙂 …
Однако, как бы то ни было, сегодня едва ли не самое главное определение для сверхзвука носит имя (точнее фамилию :-)) немца Эрнста Маха. И само по себе это слово уже давно перестало быть просто фамилией. Мах, он мах и есть 🙂 . Только скорость, только полет 🙂 …
Вернемся, тем не менее, к конкретике. Что же такое это самое число М, и зачем оно вообще-то нужно в авиации? Ведь летали же себе люди раньше на дозвуковых скоростях безо всяких чисел Маха, да и сейчас подавляющее большинство летательных аппаратов на земле — дозвуковые. Однако, не все так просто, как выглядит :-).
При любом полете аппарата тяжелее воздуха одним из самых важных его параметров является скорость. Способов измерения скорости на сегодняшний день, вобщем-то, предостаточно :-). Для примера, параметры движения самолета относительно воздушной среды можно измерить следующими способами: ультразвуковой, термодинамический, тепловой, турбинный, манометрический.
А путевую скорость (то есть скорость относительно земли) можно измерить допплеровским, корелляционным, радиационным способом, а также способом визирования земной поверхности.
Но самый, так сказать, простой и логичный, давно применяющийся, а поэтому, естественно, проработанный и привычный все же аэрометрический (точнее говоря, аэродинамический) способ. С его помощью как раз и замеряется воздушная скорость самолета и число Маха.
Однако способ этот имеет определенные недостатки. Сам принцип его достаточно прост, и о нем мы уже ранее говорили. Воздух, набегая на летательный аппарат, в результате своего движения обладает некоторой кинетической энергией или, попросту говоря, скоростным напором (ρV²/2).
Попадая в приемник воздушного давления (ПВД, или Трубку Пито) он тормозится, и его напор превращается в давление на мембрану стрелочного прибора-указателя. Чем быстрее летит самолет, тем больше скоростной напор, тем большую скорость показывает стрелка прибора. То есть, вроде бы, все как по нотам.
Но не тут-то было :-). Пока летательный аппарат летит не очень быстро ( примерно до 400 км/ч) и не слишком высоко (тысяч где-то до 2-ух, 3-х) все действительно разворачивается просто и закономерно. А далее ноты начинают врать :-)…
Воздух взаимодействует с аэродинамическими поверхностями самолета, определяя тем самым параметры его полета. А эти параметры зависят от параметров состояния воздуха, как газа, которые, конечно, зависят от условий, в которых находится данный объем газа.
Например, с высотой падают плотность и температура воздуха. А чем плотность ниже, тем меньше будет скоростной напор, с которым набегающий поток давит на мембрану указателя скорости.
То есть получается, что если прибор в кабине пилота показывает одинаковую скорость на высотах, к примеру, 2000 м и 10000 м ( приборная скорость), то на самом деле это означает, что самолет на 10000 м относительно воздуха (и земли, конечно, тоже :-)) движется значительно быстрее (истинная скорость). Все из-за того, что воздух на высоте разрежен.
Плюс еще такая, не совсем, мягко говоря, удобная для полета вещь, как сжимаемость. Воздух — это газ, и, как любой газ, его можно при определенных условиях сжать, тем самым меняя параметры его состояния. Такие условия появляются при обтекании аэродинамических поверхностей на достаточно больших скоростях полета (формально отсчет начинают от 400 км/ч).
Воздух перестает быть однородной, одинаковой во всех направлениях средой, каковой он считается (хоть и довольно приближенно) для малоскоростных летательных аппаратов. Создаются условия для возникновения так называемых скачков уплотнения, меняются скорости движения воздушного потока на различных участках аэродинамической поверхности (профиля крыла, например), происходит сдвиг точки приложения аэродинамических сил, то есть меняется сам характер обтекания и, в конечном итоге, параметры управляемости летательного аппарата. То есть говоря «умными» терминами теории сверхзвука :-), начинается волновой кризис.
Однако, о нем мы еще будем говорить в дальнейшем. А пока можно заметить, что все эти процессы зависят от параметров воздушной среды и технико-конструктивных свойств самого летательного аппарата.
Чтобы описать аэродинамические свойства самолета во взаимодействии со средой, одной скорости движения бывает недостаточно. Ведь ее измеренная величина, качественно сама зависящая от параметров этой среды, не всегда характеризует истинную картину обтекания (как в примере выше).
Здесь нужен такой критерий, который бы учитывал «в себе» параметры потока и, опираясь на который, можно было бы всегда правильно охарактеризовать аэродинамические свойства летательного аппарата вне зависимости от условий полета.
Говоря это, я как раз и имею в виду число М. И слово «критерий» употребляю не случайно. Дело в том, что число Маха – это, говоря языком физики, один из критериев подобия в газовой динамике.
Смысл этого слегка замысловатого названия на самом деле прост и заключается в том, что если две или более физические системы имеют однотипные критерии подобия, равные по величине, то это означает, что рассматриваемые системы подобны, то есть похожи или, говоря совсем упрощенно (:-)) одинаковы.
Применительно к нашему авиационному случаю это может выглядеть, например, так. Воздушный поток на двух различных высотах (допустим те же 2000 и 10000 м), взаимодействующий с нашим летательным аппаратом – это и есть две физические системы.
Однако, если приборные скорости на этих высотах одинаковы, то это вовсе не означает, что указанное взаимодействие тоже будет одинаковым, скорее как раз наоборот. То есть скорость не может быть критерием подобия, и эти две системы в такой ситуации вовсе не подобны.
Однако, если мы говорим о том, что самолет на различных высотах (и вообще в различных условиях) летит с одинаковым числом Маха, то вполне правомерно утверждать, что условия обтекания и аэродинамические свойства на этих высотах (в этих условиях) будут одинаковы.
Здесь обязательно стоит сказать, что это утверждение, несмотря на свою верность, опирается, однако, на немалые упрощения. Первое – это то, что число Маха, хоть и основной для нас критерий подобия в газодинамике, но не единственный. А второе исходит из определения самого числа М.
Эрнст Мах, проводя свои исследования, вряд ли задумывался о применении их результатов в авиации :-). Ее тогда попросту не было. Определение было чисто научным и физически точным. Число Маха – это безразмерная величина, равная отношению скорости потока в данной точке движущейся газовой среды к скорости звука в этой точке.
То есть М = V/ a, где V – скорость потока в м/с, а – скорость звука в м/с. Таким образом число М как бы учитывает в себе скорость движения плюс изменение параметров воздушной среды через скорость звука, которая как раз от этих параметров и зависит.
Число Маха величина безразмерная. В единицах скорости выразить его невозможно, и перевод его в линейную скорость нецелесообразен из-за непостоянства скорости звука. Скорость летательного аппарата, используя число М, можно выразить только качественно, то есть оценивая, во сколько раз скорость самолета больше, либо меньше скорости звука.
При этом формат записи значений может быть как с использованием знака равенства, так и без него. Например запись М3 (как и М=3) может означать, что скорость летательного аппарата превысила скорость звука в три раза.
Упрощения применительно к авиации состоят в том, что скорость потока заменена на скорость движения физического тела в газовой среде, то есть имеется в виду истинная скорость движения самолета. За скорость звука принимается скорость звука на высоте полета. При этом, однако, не учитывается, что поток возле тела сложной формы, коим летательный аппарат и является :-), может иметь самые различные значения вблизи различных участков поверхности этого тела.

Указатель числа М на приборной доске сверхзвукового "Конкорда" (правый нижний угол). Над ним указатель скорости.
Однако, несмотря на достаточную некорректность упрощений, концепция числа Маха нашла в авиации очень широкое применение. Причем не только на сверхзвуковых самолетах, для которых сведения о числе М, так сказать, жизненно необходимы :-), но и на многих дозвуковых современных самолетах.
Ведь скорости их, хоть и дозвуковые, достаточно велики. К тому же практические высоты полетов тоже немаленькие. Так как скорость звука с высотой ощутимо падает, то возникает целесообразность на больших высотах использовать при пилотировании число Маха.
Для этого есть, по крайней мере, две причины. Во-первых, из-за большой разницы приборной и истинной скоростей, о чем я упоминал выше (лишние погрешности, к тому же очень ощутимые, никому не нужны :-)), а, во-вторых, для возможности оценки приближения волнового кризиса.
Дело в том, что для каждого типа летательного аппарата его проявления имеют место при определенных значениях числа М. В связи с этим практически все современные лайнеры имеют полетные ограничения по числу Маха для обеспечения устойчивого управления. Пилот при управлении самолетом следит за тем, чтобы это ограничение не было превышено.
Таким образом число М — это не скорость в чистом виде, но, тем не менее, важный параметр, позволяющий экипажу правильно оценивать условия полета и осуществлять безопасное и точное управление летательным аппаратом.
Для получения информации о числе Маха практически все современные скоростные самолеты имеют в кабине экипажа указатель числа М. В просторечии его иногда именуют махметром. В большинстве случаев он представляет собой стрелочный указатель по типу указателя скорости. Такие приборы могут выдавать либо только значения числа Маха, либо могут быть объединены (скомбинированы) с указателем скорости, истинной или приборной.
Часто указатели числа М выполняют со специальным сигнализатором, который в нужный момент выдает предупреждение экипажу о превышении какого-либо порогового значения этого числа.
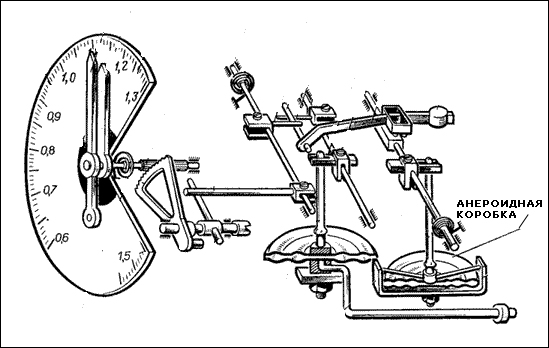
По своей конструкции и принципу действия указатель числа М вобщем-то аналогичен указателю воздушной (приборной ) скорости. Но для учета изменения условий с высотой в него добавлена анероидная коробка, реагирующая на изменение давления.
Подавляющее большинство современных самолетов летает все-таки на дозвуке. Этому режиму соответствует число Маха менее 0,8. Следующие режимы полета, на которых М принимает значения от 0,8 до 1,2 объединены под названием трансзвук. А когда число М меняется от 1,0 до 5,0, то это уже чистый сверхзвук, зона сверхзвукового полета современных военных самолетов.
Есть, правда, экземпляры напрямую к армии не относящиеся, более того достигающие скоростей, на которых число Маха превышает пять единиц. Это уже зона гиперзвука. Однако говорить об этих полуэкзотических аппаратах и режимах их полета мы будем уже в следующих статьях общей темы, посвященной сверхзвуку.
До новых встреч :-).
Фотографии кликабельны.










Спасибо
Учился ещё в 66-69гг. в Омском ОАУССГА на прибориста. В то время нам преподаватели о числе М объясняли на пальцах очень доходчиво. Рад, что в настоящее время есть люди, способные это сделать доходчиво. После окончания училища работал в Красноярской АТБ (знающий поймёт) на ИЛ-18, ТУ-154, ИЛ-76 по автопилотам и автоштурманам (спецбригада в цехе №7).
Ну зачем же передергивать! Училась в начале 80-х в МЭИ, в гидрогазодинамике число М всегда называлось числом Маха, причём учебник был далеко не новый. В остальном — отличная, очень интересная публикация ))))
Спасибо! Прочитал все на одном дыхании и все стало понятно! Еще с училища до конца не понимал число М, теперь все встало на свои места)). Успехов Юра!
Спасибо. Теперь понятно, почему не ограничиваются только приборной скоростью. Объясните, пожалуйста, почему диапазон трансзвука (0,8-1,2) попадает в сверхзвук (1,0-5,0)? Заранее благодарю за ответ.
Трансзвуковой диапазон выделен искусственно. Просто именно в этом диапазоне происходит резкий рост аэродинамического сопротивления за счет возникновения волнового кризиса. После 2М эти явления сглаживаются.
)) зависть беленькая твоей увлеченности, желанию переворачивать горы литературы, изучать, переваривать и так интересно преподносить. Мое хобби в одном флаконе с профессией… И вдруг… стало неинтересно… Неиссякаемости твоему научному творчеству!
У старины Маха теория научного творчества через ощущения… У меня ощущения благодаря твоему научному творчеству…. Спасибо, Юра.
Не за что :-)! Надеюсь ощущения приятные….
Юрий, а где статья Сверхзвук, часть 1 ?
Все то же извинение за задержку :-)… Статья здесь. Мой плагин похожих статей отвратительно работает. Должен указывать в конце каждой статьи похожие на нее, но не делает этого почему-то. Поправлю в конце декабря, там будет на это время (праздники все-таки :-))…
Мне нравится ваш стиль изложения материала. Веду раздел «Авиационные семинары» на русскоязычном форуме и хотел бы иногда использовать ваши статьи. В какой форме это было бы возможно?
Вобщем-то в любой форме. Для меня важно только, чтобы было конкретное упоминание о ресурсе, с которого взят материал, то есть мой сайт http://avia-simply.ru/ и на видном месте прямая ссылка на статью.
Интересно, что это за форум с таким любопытным разделом… Могу я туда попасть? Люблю такие ресурсы :-)…
Будем рады!
http://aviaforum.net/forum/14
Мой ник — adzyga
Логин скайпа — adzyga1
PS.
Сообщение #65:
http://aviaforum.net/forum/14-726-4#31582
🙂
Прошу прощения, что недостаточно четко сформулировал свою мысль.
Именно о замене названия «приборная скорость» я и хотел сказать.
:-)… Интересно, что у меня после размещения ответа на Ваш комментарий появилась мысль о том, что Вы вовсе не теоретические основы имеете ввиду, а именно вопрос названий, но все же засомневался и оставил все как есть. Видимо зря :-)… Да, я с вами согласен насчет того, что понятие «приборная» уже не соответствует тому смыслу, который в него первоначально вкладывался. Но в обозримом будущем, конечно, вряд ли что-то изменится :-)…
ИМХО. Разделение скоростей на истинную (TAS) и приборную (IAS) было оправдано тогда, когда прибор скорости (УС) измерял только скоростной напор, а истинная скорость рассчитывалась.
С внедрением комбинированных указателей скоростей (КУС), учитывающих изменение давления с высотой и температуру наружного воздуха, обе эти скорости могут считаться приборными. Следовательно, прилагательное «приборная» можно было бы и опустить. Но тогда для IAS следует подыскать более подходящее название. 🙂
Позволю себе с Вами не согласиться. Приборная и истинная скорости, хоть и измеряются (показываются) одним и тем же прибором (КУС), но имеют разное назначение (и использование). Приборная, тот самый скоростной напор, нужна для пилотирования «здесь и сейчас». Она характеризует взаимодействие летательного аппарата с набегающим потоком в данной точке пространства и в данный момент времени, то есть несущие свойства планера, что нужно для правильного и безопасного пилотажа, взлета и посадки и т.д. Истинная же скорость вместе со своими поправками этой картины не дает и предназначение у нее другое — самолетовождение (не местное пилотирование!). Поэтому разделение этих скоростей все так же актуально. А вот насчет названий можно было бы поразмыслить :-). Лично мне (ИМХО), само слово «приборная» как-то не очень нравится, да и вообще названий хватает, как и разнобоя в определениях даже среди летного состава (почитал по форумам) :-)….
КУС (комбинированный указатель скорости) совмещает на одной шкале две стрелки — широкую(приборная скорость — для пилотирования) и узкую (истинная — для самолетовождения по-старому или навигации). Вы правы, прилагательное «приборная» тстарое, радиционное, лучше, конечно, назвать ее «пилотажная».
Да, действительно. Определение «пилотажная» было бы более правильно в нынешней ситуации.
Сжимаемость воздуха и волновой кризис (смещение центра давления разных профилей крыла и изменение продольного момента крыла для безопасности полета) начинается с М=0,8-0,85, что соответствует приборной скорости приблизительно 800-900км\час в зависимости от высоты полета. На этих скоростях у самолетов с прямым крылом проявлялся опасный эффект — «затягивание в пикирование» из-за резкого смещения фокуса профиля назад относительно постоянного центра тяжести самолета. По этой причине и разбился самолет БИ-1, погиб летчик-испытатель Бахчиванджи, пока не применили крыло стреловидной формы, у которого этот эффект не так критичен, более плавное смещение центра давления. Он стабилизировался после числа М=1,05. Т.е. фокус профиля занимает постоянное место и «хватает» рулей для горизонтального полета.
Совершенно с Вами согласен. Об этом я упомянул в этой статье.
Чем отличается ПРИБОРНАЯ (относительно частиц воздуха) скорость от ИСТИННОЙ (относительно земной поверхности)?
ПРИБОРНАЯ скорость нужна для техники пилотирования и для безопасности полетов — чтоб выполнять элементы полета (взлет, набор, снижение) или фигуры пилотажа (петли, боевые развороты, виражи и т.д.), чтоб не сорваться в штопор.
ИСТИННАЯ — для самолетовождения, т.е. расчетов времени нахождения в воздухе, перелета и прибытия из пункта А в пункт Б, выхода на цель в заданное время.
В плане использования скоростей все правильно, только истинная скорость — это скорость не относительно земной поверхности, а относительно всей массы воздуха, в которой находится самолет. Относительно земли — это путевая скорость. Об этом я упоминал здесь. Приборную скорость мы видим на приборе, когда на его мембрану давит воздух определенной плотности, на данной высоте. То есть, так сказать, местная скорость, удобно для пилотирования «здесь и сейчас». Но с высотой плотность воздуха падает и, если прибор на высоте показывает ту же скорость, что и у земли, то это значит, что относительно всей массы воздуха самолет летит быстрее, ведь при меньшей плотности ему надо лететь быстрее, чтобы получить ту же силу давления на мембрану прибора. Как-то так :-)…
ПУТЕВАЯ скорость — это истинная с поправкой на ветер (из навигационного треугольника скоростей), а «относительно всей массы воздуха» — это приборная, которая «давит на мембрану». В истребителях приборную скорость показывает широкая стрелка, истинную- узкая, а путевая — «в уме» (высчитывается).
Верно, путевая скорость — это истинная с поправкой на ветер, то есть скорость относительно земли. Она «в уме», то есть вычисляется. Но «относительно всей массы воздуха» или по-другому фактическая относительно воздуха — это не приборная, а истинная. Ее хоть и показывает на КУСе узкая стрелка (не только, кстати, на истребителях), но показания эти — это не тот скоростной напор, который «давит на мембрану» и дает нам приборную (по определению) скорость, которую Вы назвали «пилотажной»(на мой взгляд очень правильно). Это напор плюс поправка на плотность, плюс на некоторых КУСах температурная поправка. Остальные поправки «в уме» :-)…
Название где-то слышала, теперь буду знать что это такое и где применяется, очень интересно, о зоне гиперзвука даже не слышала, сколько у Вас познавательного.
К своему стыду, я до нынешнего дня о числе М понятия не имела!
:-))) Ну и ничего страшного… Теперь будете знать…
Слышал об этом термине, но не думал что это фамилия ученого, думал это связано с каким то махом=))))
О! Спасибо =) Видимо, для этого пилотам нужно давление знать?
Пилотам при пилотировании, вобщем-то, необязательно. Давление учитывается прибором (анероидная коробка, в частности, для этого) и на указателе уже готовое число М. А уж с учетом его величины и производится управление….
Да, я как раз об этом. Не конкретно для управления, а да установки точки отсчета прибору.
Тут как раз точка отсчета не нужна, как это, например, делается для барометрического высотомера, где определяется нулевая (исходная) высота места. Число М определяется для данных, конкретных условий и эти условия характеризует. Если этот момент не понятен, напишите — разберемся :-)…
Спасибо за статью. Как всегда, очень интересно и познавательно.